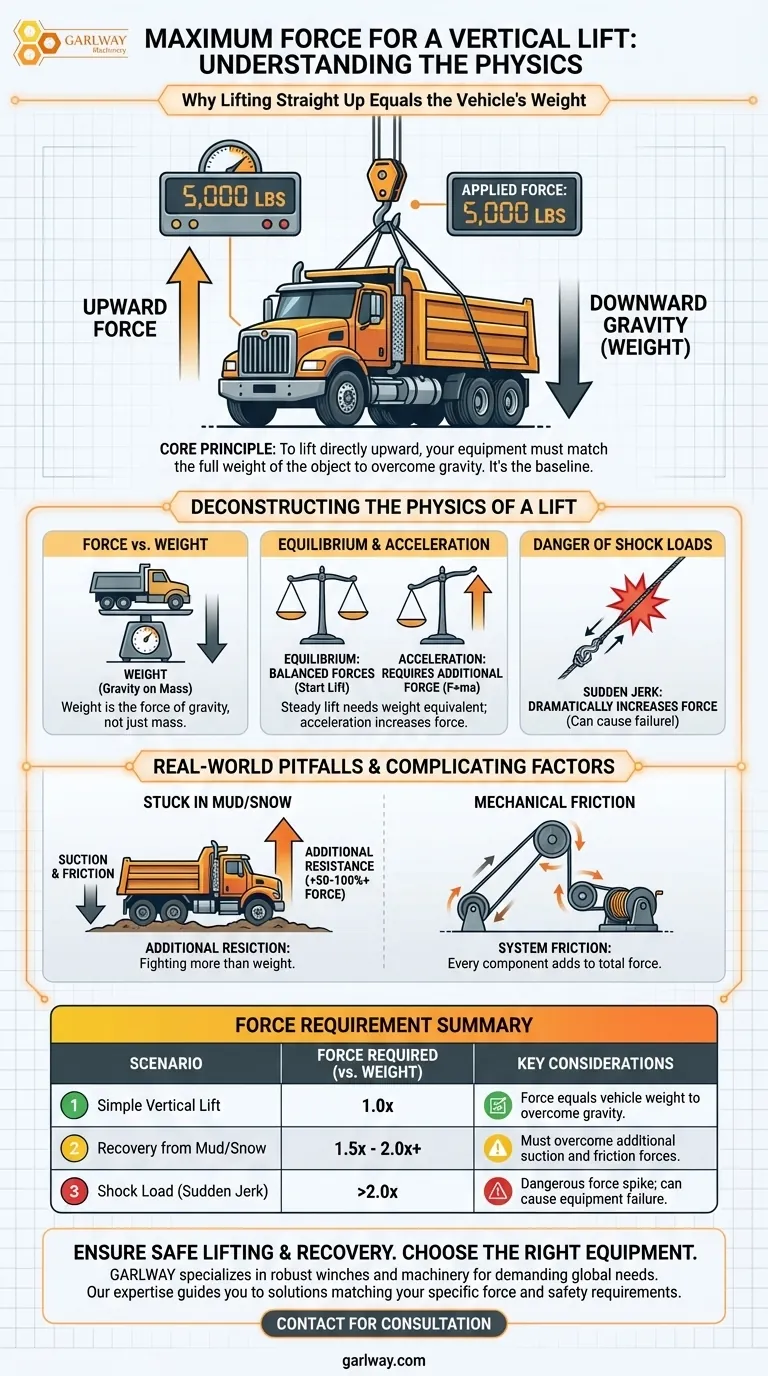
最简单地说,向上垂直拉起车辆所需的最大力等于车辆自身的重量。如果一辆卡车重 5,000 磅,您只需施加 5,000 磅的向上力就可以将其从地面抬起。
要克服直接垂直起重中的重力,您的设备必须能够承受物体的全部重量。这是物理学的一项基本原理,构成了任何起重或救援计算的基础。
解析垂直起重的物理学原理
理解所需力为何等于车辆的重量对于安全有效地操作至关重要。这不仅仅是一个经验法则;它是核心物理学原理的直接应用。
力与重量:核心关系
车辆的重量是作用在其质量上的重力的大小。它本身并不等同于质量。
当您抬起车辆时,您施加了一个向上的力来抵消重力(其重量)向下的力。
平衡的概念
要开始起重,您必须施加至少等于车辆重量的力。这会产生一个平衡状态,其中向上的力和向下的力(重力)是平衡的。
要实现实际的向上运动,施加的力必须比车辆的重量大无穷小。对于所有关于设备容量的实际计算,我们认为最大所需力是车辆重量的 1.0 倍。
加速度的关键作用
牛顿第二定律(力 = 质量 × 加速度)告诉我们,任何向上的加速度都需要额外的力。
缓慢稳定地起重车辆需要等于其重量的力。然而,猛拉绳索或试图快速起重会大大增加所需的力,从而产生危险的“冲击载荷”。

常见陷阱和复杂因素
虽然简单垂直起重的物理学原理很简单,但现实情况很少是完美的。有几个因素会使所需力远远超过车辆的整备质量。
冲击载荷的危险
救援绳索上的突然拉动或“冲刺”会成倍增加施加在系统上的力。这种冲击载荷很容易超过绞车、绳索和连接点的额定工作载荷,导致灾难性故障。
卡住造成的阻力
如果车辆陷入泥、沙或雪中,您要对抗的不仅仅是它的重量。您还必须克服强大的吸力和摩擦力。
与简单起重相比,这种额外的阻力很容易使救援所需的力增加 50% 至 100%(甚至更多)。
系统中的机械摩擦
您索具设置中的每个滑轮、滑块或方向变化都会产生摩擦。虽然通常很小,但这种摩擦会增加绞车或起重机构为移动负载必须产生的总力。
为您的任务做出正确选择
利用对力的理解来选择正确的设备和策略。您的主要目标决定了您应该如何解释“1.0 倍车辆重量”的规则。
- 如果您的主要重点是简单、受控的垂直起重:您的设备(起重机、绞车等)必须具有至少等于车辆全部重量的额定工作载荷。
- 如果您的主要重点是从泥泞或雪地中救援:假设所需的力将显著高于车辆的重量,并使用具有较大安全系数的设备(例如,额定载荷为车辆重量 1.5 倍至 2.0 倍的绞车)。
- 如果您的主要重点是任何情况下的安全:始终缓慢平稳地操作,以避免对设备造成冲击载荷。
理解这一基本原理,使您能够安全有效地规划您的操作。
总结表:
| 场景 | 所需力(相对于车辆重量) | 关键考虑因素 |
|---|---|---|
| 简单垂直起重 | 1.0 倍 | 力等于车辆重量以克服重力。 |
| 从泥泞/雪地中救援 | 1.5 倍 - 2.0 倍+ | 必须克服额外的吸力和摩擦力。 |
| 冲击载荷(突然拉动) | >2.0 倍 | 危险的力峰值;可能导致设备故障。 |
确保您的起重和救援操作安全有效
选择正确的设备至关重要。本文中的力计算是选择具有适当容量和安全裕度的绞车和其他机械的基础。
GARLWAY 专注于提供坚固的建筑机械,包括强大的绞车、混凝土搅拌机和配料厂,专为全球建筑公司和承包商的严苛需求而设计。
让我们的专业知识指导您找到正确的解决方案。立即联系我们的团队,就符合您特定力学和安全要求的设备进行咨询。
图解指南